Đề Kiểm Tra: Trắc Nghiệm Bài 15 Hàm Số Online Có Đáp Án Và Lời Giải-Đề 1 Câu 1: Tập xác định của hàm số \(y = {x^2} – 2024x + 2025\) là
\(\left( { - \infty ;\, + \infty } \right)\).
Gợi ý Hàm số là hàm đa thức nên xác định với mọi số thực \(x\).
Câu 2: Tập xác định của hàm số \(y = \frac{{x – 3}}{{4x – 4}}\) là
\(\mathbb{R}\backslash \left\{ 1 \right\}\).
Gợi ý Điều kiện xác định : \(4x – 4 \ne 0 \Leftrightarrow x \ne 1\)
Câu 3: Tập xác định của hàm số \(y = \frac{{2025}}{{{x^2} – 9}}\) là
\(\mathbb{R}\backslash \left\{ { - 3;3} \right\}\).
Gợi ý Hàm số đã cho xác định khi \({x^2} – 9 \ne 0 \Leftrightarrow \left\{ \begin{gathered} x \ne 3 \hfill \\ x \ne – 3 \hfill \\ \end{gathered} \right.\).
Câu 4: Tập xác định \(D\) của hàm số \(y = \sqrt {3x – 1} \) là
\(D = \left[ {\frac{1}{3}; + \infty } \right)\).
Gợi ý Hàm số \(y = \sqrt {3x – 1} \) xác định \( \Leftrightarrow 3x – 1 \geqslant 0 \Leftrightarrow x \geqslant \frac{1}{3}\).
Câu 5: Tập xác định của hàm số \(y = \sqrt {4 – x} + \sqrt {x – 2} \) là
\(D = \left[ {2;4} \right]\)
Gợi ý Điều kiện: \(\left\{ \begin{gathered} 4 – x \geqslant 0 \hfill \\ x – 2 \geqslant 0 \hfill \\ \end{gathered} \right.\) \( \Leftrightarrow \left\{ \begin{gathered} x \leqslant 4 \hfill \\ x \geqslant 2 \hfill \\ \end{gathered} \right.\) suy ra TXĐ: \(D = \left[ {2;4} \right]\).
Câu 6: Tập xác định của hàm số \(y = \sqrt {9 – x} + \frac{x}{{\sqrt {x – 1} }}\) là \(\left( {a;b} \right]\) với \(a,b\) là các số thực. Tính tổng \(a + b\).
Gợi ý Điều kiện xác định: \(\left\{ {\begin{array}{*{20}{l}} {9 – x \geqslant 0} \\ {x – 1 > 0} \end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}} {x \leqslant 9} \\ {x > 1} \end{array}} \right.\)\( \Leftrightarrow 1 < x \leqslant 9\).
Câu 7: Với giá trị nào của \(m\) thì hàm số \(y = \frac{{2x + 1}}{{{x^2} – 2x – 3 – m}}\) xác định trên \(\mathbb{R}\).
Gợi ý Hàm số \(y = \frac{{2x + 1}}{{{x^2} – 2x – 3 – m}}\) xác định trên \(\mathbb{R}\) \( \Leftrightarrow {x^2} – 2x – 3 – m \ne 0,\,\forall x \in \mathbb{R}\)
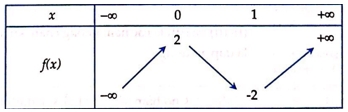
Câu 8: Cho hàm số \(f\left( x \right)\) có bảng biến thiên như sau
Gợi ý Ta thấy trong khoảng \(\left( {0;1} \right)\), mũi tên có chiều đi xuống. Do đó hàm số nghịch biến trong khoảng \(\left( {0;1} \right)\).
Câu 9: Cho hàm số có đồ thị như hình bên dưới.
Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
Gợi ý Trên khoảng \(\left( {0;2} \right)\), đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Câu 10: Cho \((P)\) có phương trình \(y = {x^2} – 2x + 4\). Điểm nào sau đây thuộc đồ thị \((P)\).
\(M\left( { - 3;19} \right)\).
Gợi ý A. \(Q\left( {4;2} \right)\).Thay \(x = 4\) vào phương trình của \((P)\) ta được \(y = {4^2} – 2.2 + 4 = 8 \ne 2\)
Kết thúc bài làm Các lựa chọn đã được chọn: Kết quả:
Câu 1 Câu 2 Câu 3 Câu 4 Câu 5 Câu 6 Câu 7 Câu 8 Câu 9 Câu 10 Đáp án: Trắc Nghiệm Bài 15 Hàm Số Online Có Đáp Án Và Lời Giải-Đề 1 Đáp án câu 1:
D \(\left( { - \infty ;\, + \infty } \right)\).
Đáp án câu 2:
A \(\mathbb{R}\backslash \left\{ 1 \right\}\).
Đáp án câu 3:
B \(\mathbb{R}\backslash \left\{ { - 3;3} \right\}\).
Đáp án câu 4:
C \(D = \left[ {\frac{1}{3}; + \infty } \right)\).
Đáp án câu 5:
B \(D = \left[ {2;4} \right]\)
Đáp án câu 8:
D \(\left( {0;1} \right)\)
Đáp án câu 9:
C Hàm số nghịch biến trên khoảng \(\left( {0;2} \right)\).
Đáp án câu 10:
D \(M\left( { - 3;19} \right)\).
Xem thêm: Đáp án Trắc Nghiệm Bài 15 Hàm Số Online Có Đáp Án Và Lời Giải-Đề 1 mới nhất.
Hàm số nghịch biến trong khoảng nào dưới đây?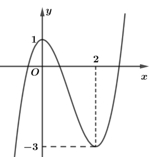
Khẳng định nào sau đây là đúng?